پاسخ : پردازش تصویر،از صفر تا هر جا که همکاری کنین ...
>> reza1b=medfilt2(reza1n);
??? A must be a 2-D real uint8, uint16, or double array.
Error in ==> C:\MATLAB6p1\toolbox\images\images\private\ordfa.d ll
Error in ==> C:\MATLAB6p1\toolbox\images\images\ordfilt2.m
On line 67 ==> B = ordfa(A, order, offsets, [padSize padSize] + 1, originalSize);
Error in ==> C:\MATLAB6p1\toolbox\images\images\medfilt2.m
On line 53 ==> b = ordfilt2(a, order, domain, padopt);
اگه میشه بگین دستور من چه ایرادی داره که این پیقامو داده
و بگین چه جوری میشه با مطلب از پورت پرینتر خروجی گرفت
واقیاتش یه موضوع در این مورد تو سایت بود که نتونستم بازش کنم
>> reza1b=medfilt2(reza1n);
??? A must be a 2-D real uint8, uint16, or double array.
Error in ==> C:\MATLAB6p1\toolbox\images\images\private\ordfa.d ll
Error in ==> C:\MATLAB6p1\toolbox\images\images\ordfilt2.m
On line 67 ==> B = ordfa(A, order, offsets, [padSize padSize] + 1, originalSize);
Error in ==> C:\MATLAB6p1\toolbox\images\images\medfilt2.m
On line 53 ==> b = ordfilt2(a, order, domain, padopt);
اگه میشه بگین دستور من چه ایرادی داره که این پیقامو داده
و بگین چه جوری میشه با مطلب از پورت پرینتر خروجی گرفت
واقیاتش یه موضوع در این مورد تو سایت بود که نتونستم بازش کنم









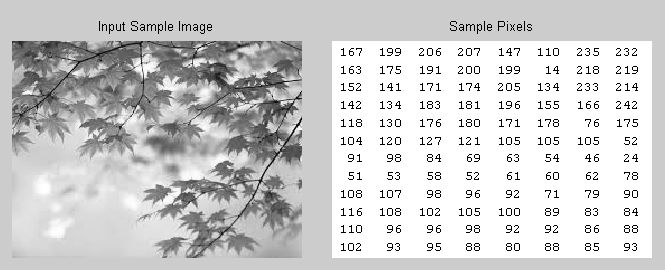




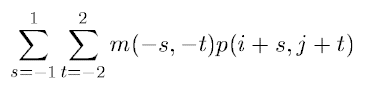
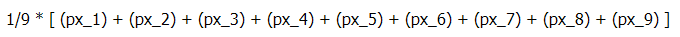




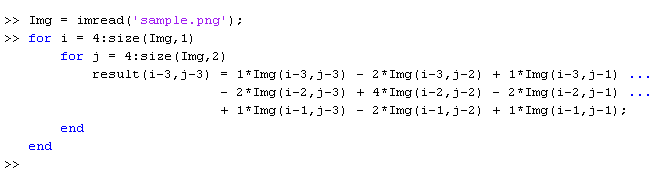






























دیدگاه